10 Review of Statistics

import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='darkgrid') # Set the style of plots
from scipy.integrate import quad

\[ \DeclareMathOperator{\cov}{cov} \DeclareMathOperator{\corr}{corr} \DeclareMathOperator{\var}{var} \DeclareMathOperator{\SE}{SE} \DeclareMathOperator{\E}{E} \DeclareMathOperator{\A}{\boldsymbol{A}} \DeclareMathOperator{\x}{\boldsymbol{x}} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\argmin}{argmin} \newcommand{\tr}{\text{tr}} \newcommand{\bs}{\boldsymbol} \newcommand{\mb}{\mathbb} \]

10.1 Estimators and their properties

Let $Y_1, Y_2, \dots, Y_n$ be an i.i.d. random sample from a population distribution with mean $\mu_Y$ and variance $\sigma_Y^2$. We aim to use this sample to learn about unknown characteristics of the population distribution, such as its mean, variance, and other parameters. To achieve this, we construct estimators.

Definition 10.1 (Estimator and estimate) An estimator is a statistic formulated from $\{Y_1,Y_2,\dots,Y_n\}$ to estimate an unknown characteristic of the population distribution. An estimate is the numerical value obtained by computing the estimator using data from a specific sample.

Note that an estimator is a random variable because it is formulated from the sample $\{Y_1,Y_2,\dots,Y_n\}$, which is a random sample. On the other hand, an estimate is a constant because it is computed from the realization of a specific sample $\{Y_1,Y_2,\dots,Y_n\}$, i.e., it is a realization of the estimator.

Example 10.1 If the unknown characteristic is the population mean $\mu_Y$, then the estimator of $\mu_Y$ is a statistic formulated from $\{Y_1,Y_2,\dots,Y_n\}$, such as $\hat{\mu}_Y=\bar{Y}=\frac{1}{n}\sum_{i=1}^nY_i$. The estimate of $\mu_Y$ is the numerical value of $\hat{\mu}_Y$ when it is computed using data from a specific sample, e.g., $\hat{\mu}_Y=5.2$.

Since estimators are random variables, they have associated probability distributions, known as sampling distributions.

Definition 10.2 (Sampling distribution of an estimator) Let $\hat{\mu}_Y$ be an estimator of the population parameter $\mu_Y$. The probability distribution of $\hat{\mu}_Y$ is called the sampling distribution of $\hat{\mu}_Y$.

Intuitively, the sampling distribution of an estimator is the probability distribution obtained by computing the estimator across all possible samples of size $n$ drawn from the population. It provides insight into how the estimator behaves across different samples and is essential for understanding its properties, such as bias, consistency, and efficiency.

Definition 10.3 (Properties of an estimator) Let $\hat{\mu}_Y$ be an estimator of the population parameter $\mu_Y$.

We say that $\hat{\mu}_Y$ is unbiased estimator if $\E(\hat{\mu}_Y)=\mu_Y$.
We say that $\hat{\mu}_Y$ is a consistent estimator if $\hat{\mu}_Y\xrightarrow{p}\mu_Y$ as the sample size tends to infinity.
Let $\tilde{\mu}_Y$ be another estimator of $\mu_Y$, and suppose that both $\hat{\mu}_Y$ and $\tilde{\mu}_Y$ are unbiased. Then, $\hat{\mu}_Y$ said to be more efficient (or precise) than $\tilde{\mu}_Y$ if $\text{var}(\hat{\mu}_Y) < \text{var}(\tilde{\mu}_Y)$.

The unbiasedness property implies that the sampling distribution of the estimator $\hat{\mu}_Y$ is centered around the true value of the population parameter $\mu_Y$. The bias of $\hat{\mu}_Y$ is defined as $\text{Bias}(\hat{\mu}_Y) = \mathbb{E}(\hat{\mu}_Y) - \mu_Y$. The consistency property indicates that as the sample size increases, the sampling distribution of $\hat{\mu}_Y$ becomes increasingly concentrated around the true value $\mu_Y$. Among all unbiased and consistent estimators, we prefer the one with the smallest variance, known as the most efficient estimator.

Example 10.2 Let $\hat{\mu}_1$ and $\hat{\mu}_2$ be two unbiased estimators of $\mu_Y = 5$. Assume that the sampling distribution of $\hat{\mu}_1$ is $N(5, 0.5)$ and that of $\hat{\mu}_2$ is $N(5, 1)$. Then, we have $\mathbb{E}(\hat{\mu}_1) = \mathbb{E}(\hat{\mu}_2) = 5$, indicating that both estimators are unbiased. However, $\hat{\mu}_1$ is more efficient than $\hat{\mu}_2$ because $\text{Var}(\hat{\mu}_1) = 0.5 < \text{Var}(\hat{\mu}_2) = 1$. In Figure 10.1, we plot the sampling distributions of $\hat{\mu}_1$ and $\hat{\mu}_2$. Although both sampling distributions are centered at $\mu_Y$, the sampling distribution of $\hat{\mu}_1$ is more concentrated around $\mu_Y$ than that of $\hat{\mu}_2$, indicating that $\hat{\mu}_1$ is more efficient than $\hat{\mu}_2$.

# The sampling distributions of two estimators
x = np.linspace(2, 8, 500)
mu_Y = 5

pdf1 = stats.norm.pdf(x, loc=mu_Y, scale=0.5)
pdf2 = stats.norm.pdf(x, loc=mu_Y, scale=1)

fig, ax = plt.subplots(figsize=(5, 4))
ax.plot(x, pdf1, label=r'$\hat{\mu}_1$', color='steelblue', linewidth=2)
ax.plot(x, pdf2, label=r'$\hat{\mu}_2$', color='black', linewidth=2)
ax.axvline(mu_Y, color='red', linestyle='--', linewidth=1.5, label=r'$\mu_Y=5$')
ax.axhline(0, color='gray', linestyle='--', linewidth=1)  # Add y=0 line
ax.set_xlabel('Estimates')
ax.set_ylabel('Density')
ax.legend(frameon=False)
plt.tight_layout()
plt.show()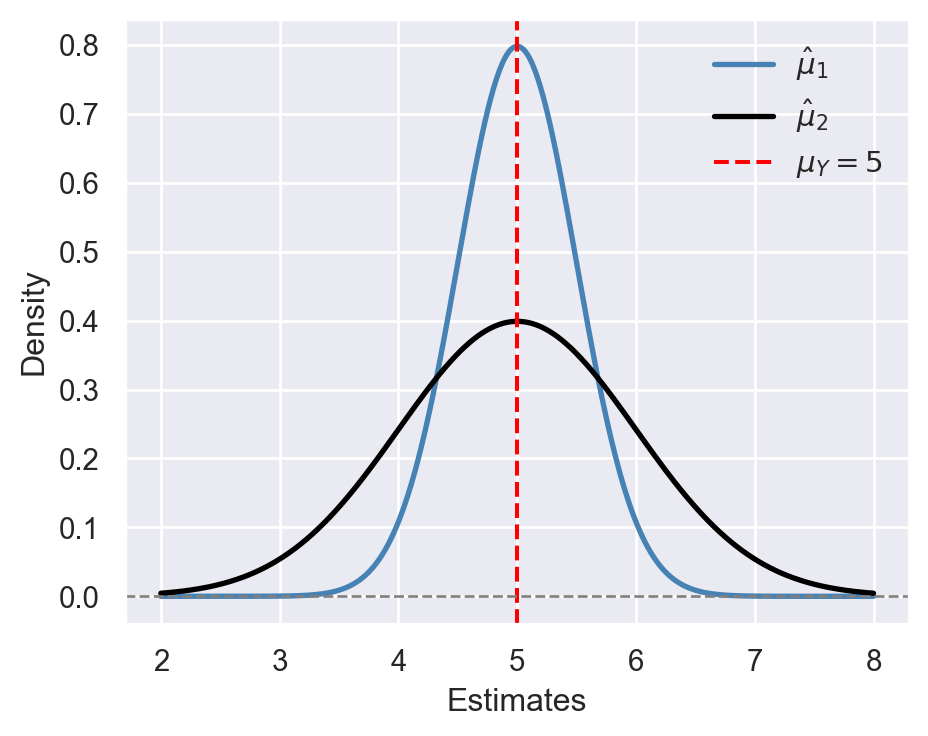

Figure 10.1: The sampling distributions of two estimators

Among the biased estimators, we may choose the one that minimizes the mean squared error (MSE), which is defined as $\text{MSE}(\hat{\mu}_Y) = \E((\hat{\mu}_Y - \mu_Y)^2)$. The MSE provides a measure of the average squared deviation of the estimator $\hat{\mu}_Y$ from the true value $\mu_Y$. It can be decomposed into the variance and the square of the bias: \[ \begin{align*} \text{MSE}(\hat{\mu}_Y) &= \E((\hat{\mu}_Y - \mu_Y)^2) = \E((\hat{\mu}_Y - \E(\hat{\mu}_Y) + \E(\hat{\mu}_Y) - \mu_Y)^2)\\ &= \E((\hat{\mu}_Y - \E(\hat{\mu}_Y))^2) + 2\E((\hat{\mu}_Y - \E(\hat{\mu}_Y))(\E(\hat{\mu}_Y) - \mu_Y)) + (\E(\hat{\mu}_Y) - \mu_Y)^2\\ &= \text{var}(\hat{\mu}_Y) + \text{Bias}^2(\hat{\mu}_Y). \end{align*} \]

10.2 Estimation of the population mean

Let $Y_1,Y_2,\dots,Y_n$ be i.i.d. random variables from a population that has mean $\mu_Y$ and variance $\sigma_Y^2$. In Chapter 9, we show that $\E(\bar{Y})=\mu_Y$ and $\text{var}(\bar{Y})=\sigma^2_Y/n$. Thus, $\bar{Y}$ is an unbiased estimator of $\mu_Y$ and a consistent estimator of $\mu_Y$ by the law of large numbers. Thus, we have $\text{MSE}(\bar{Y}) = \text{var}(\bar{Y}) = \sigma^2_Y/n$, which converges to $0$ as $n\to\infty$. Stock and Watson (2020) show that $\bar{Y}$ is the most efficient estimator among the estimators that are formulated as a linear function of $Y_1,Y_2,\dots,Y_n$.

Key Concept 10.1: $\bar{Y}$ is the Best Linear Unbiased Estimator (BLUE) of $\mu_Y$

Let $\tilde{\mu}_Y=\sum_{i=1}^na_iY_i$ be an unbiased estimator of $\mu_Y$, where $a_1,\dots,a_n$ are nonrandom constant. Then, $\text{var}(\bar{Y})<\text{var}(\tilde{\mu}_Y)$. Therefore, $\bar{Y}$ is the Best Linear Unbiased Estimator (BLUE) of $\mu_Y$, meaning it is the most efficient estimator among all unbiased estimators that are linear functions of $Y_1,Y_2,\dots,Y_n$.

In Key Concept 10.1, we claim that $\bar{Y}$ is the most efficient estimator among all unbiased estimators that are linear functions of $Y_1,Y_2,\dots,Y_n$. Hansen (2022) shows that $\bar{Y}$ is the most efficient estimator among all unbiased estimators, including those that are nonlinear functions of $Y_1,Y_2,\dots,Y_n$.

Example 10.3 Let $Y_1$, $Y_2$ and $Y_3$ be a random sample from $\chi^2_m$. We consider the following four estimators for estimating $m$: $\hat{m}_1=Y_1$, $\hat{m}_2=\frac{Y_1+Y_2}{2}$, $\hat{m}_3=\frac{Y_1+2Y_2}{3}$, and $\hat{m}_4=\bar{Y}$. Note that if $Y\sim\chi^2_m$, then $\E(Y)=m$ and $\text{var}(Y)=2m$. Using these two moments, we can show the following properties:

$\E(\hat{m}_1)=\E(Y_1)=m$ and $\var(\hat{m}_1)=\var(Y_1)=2m$.
$\E(\hat{m}_2)=\frac{\E(Y_1)+\E(Y_2)}{2}=m$ and $\var(\hat{m}_2)=\frac{\var(Y_1)+\var(Y_2)}{4}=m$.
$\E(\hat{m}_3)=\frac{\E(Y_1)+2\E(Y_2)}{3}=m$ and $\var(\hat{m}_3)=\frac{\var(Y_1)+4\var(Y_2)}{9}=10m/9$.
$\E(\hat{m}_4)=\frac{\E(Y_1+Y_2+Y_3)}{3}=m$ and $\var(\hat{m}_4)=\frac{\var(Y_1)+\var(Y_2)+\var(Y_3)}{9}=6m/9$.

All four estimators are unbiased, with $\hat{m}_4$ being the most efficient. In the following code chunk, we resample $Y_1$, $Y_2$, and $Y_3$ from the $\chi^2_3$ distribution $1000$ times and compute each estimator for every resample. Figure 10.2 illustrates the sampling distribution of each estimator. As all estimators are unbiased, their estimated means are close to $m = 3$. The figure also shows that $\hat{m}_4$ is relatively more efficient, as its sampling distribution is more tightly clustered around its mean.

# The sampling distributions of estimators
# Set random seed for reproducibility
np.random.seed(12345)
r = 1000
m = 3
m1 = np.zeros(r)
m2 = np.zeros(r)
m3 = np.zeros(r)
m4 = np.zeros(r)

for i in range(r):
    data = np.random.chisquare(df=m, size=3)  # chi-squared distribution with 3 degrees of freedom
    m1[i] = data[0]
    m2[i] = (data[0] + data[1]) / 2
    m3[i] = (data[0] + 2 * data[1]) / 3
    m4[i] = np.mean(data)

# Calculate means
mean_m1 = np.mean(m1)
mean_m2 = np.mean(m2)
mean_m3 = np.mean(m3)
mean_m4 = np.mean(m4)

# Create histograms
fig, axs = plt.subplots(2, 2)

# Function to plot histogram with a vertical line at mean
def plot_histogram(ax, data, xlabel, mean_value):
    ax.hist(data, bins=30, color='steelblue', edgecolor='black')
    ax.set_xlabel(xlabel)
    ax.set_xlim(0,18)
    ax.set_ylabel('Frequency')
    ax.axvline(x=mean_value, color='red', linestyle='--', linewidth=1.5, label=f'Mean = {mean_value:.2f}')  # Solid vertical line at mean
    ax.legend(frameon=False)

# Plot histograms
plot_histogram(axs[0, 0], m1, '$\\hat{m}_1$', mean_m1)
plot_histogram(axs[0, 1], m2, '$\\hat{m}_2$', mean_m2)
plot_histogram(axs[1, 0], m3, '$\\hat{m}_3$', mean_m3)
plot_histogram(axs[1, 1], m4, '$\\hat{m}_4$', mean_m4)

# Adjust layout
plt.tight_layout()
plt.show()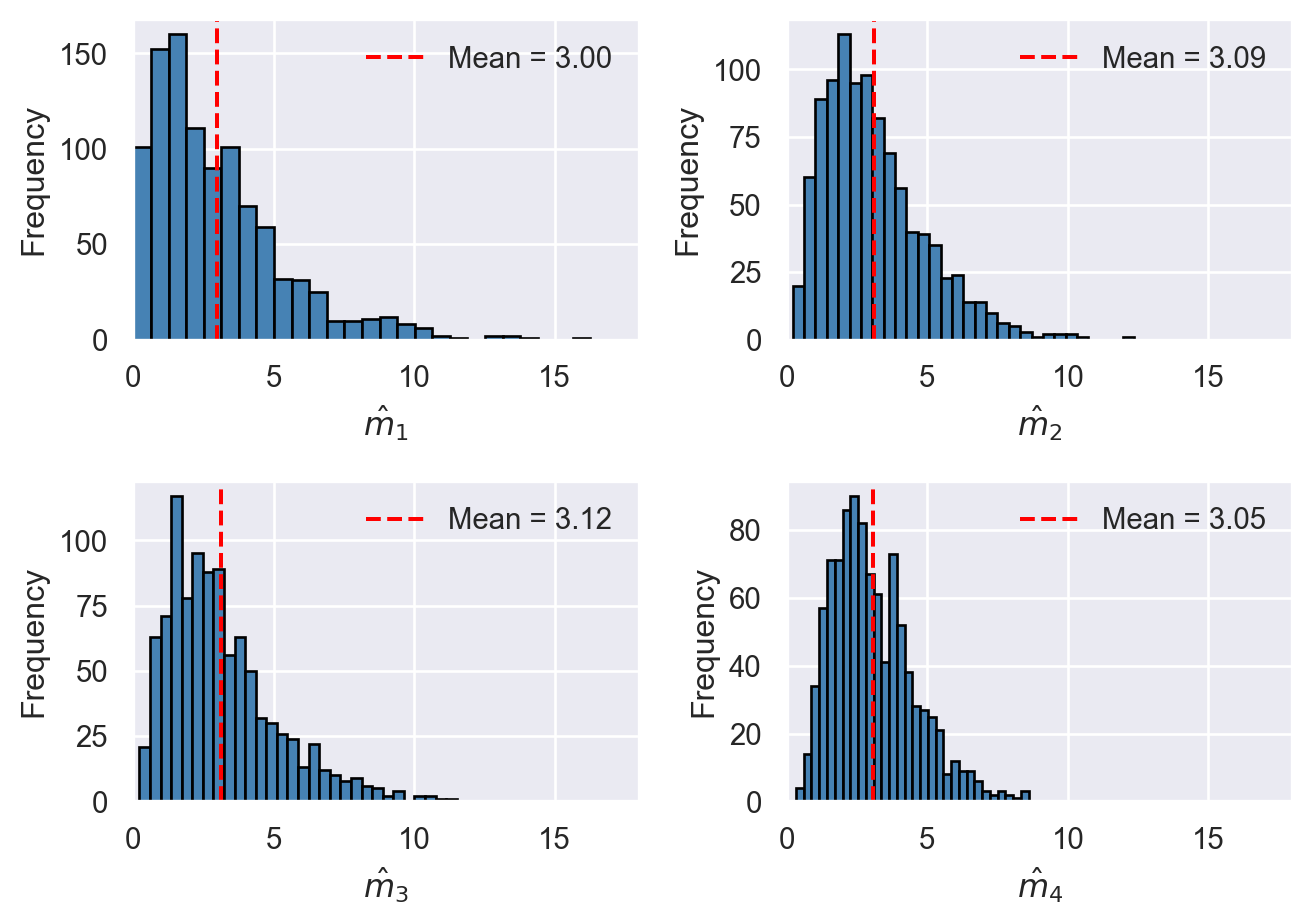

Figure 10.2: The sampling distributions of estimators

10.3 Estimation of the population variance

Let $Y_1,Y_2,\dots,Y_n$ be i.i.d. random variables with $\E(Y_i)=\mu_Y$, $\var(Y_i)=\sigma^2_Y$, and $\E(Y^4_i)<\infty$. Consider the sample variance given by \[ s^2_Y=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\bar{Y})^2. \]

We first show that $\E(s^2_Y)=\sigma^2_Y$ and then use the law of large numbers introduced in Chapter 9 to show that $s^2_Y\xrightarrow{p}\sigma^2_Y$.

First, note that $\sum_{i=1}^n(Y_i-\bar{Y})^2=\sum_{i=1}^nY^2_i-n\bar{Y}^2$. Then, we can express $\E(s^2_Y)$ as \[ \begin{align*} \E(s^2_Y)&=\E\left(\frac{1}{n-1}\sum_{i=1}^n(Y_i-\bar{Y})^2\right)=\frac{1}{n-1}\E\left(\sum_{i=1}^nY^2_i-n\bar{Y}^2\right)\\ &=\frac{1}{n-1}\left(\E\left(\sum_{i=1}^nY^2_i\right)-n\E(\bar{Y}^2)\right). \end{align*} \]

The variance computation formula $\var(Y_i)=\E(Y^2_i)-(\E(Y_i))^2$ gives $\E(Y^2_i)=\sigma^2_Y+\mu^2_Y$. Then, we have the following two expectations: \[ \begin{align*} &(1)\, \E\left(\sum_{i=1}^nY^2_i\right)=\sum_{i=1}^n\E\left(Y^2_i\right)=\sum_{i=1}^n\left(\var(Y_i)+\left(\E(Y_i)\right)^2\right)=n(\sigma^2_Y+\mu^2_Y),\\ &(2)\,\E(\bar{Y}^2)=\var(\bar{Y})+\left(\E(\bar{Y})\right)^2=\frac{\sigma^2_Y}{n}+\mu^2_Y. \end{align*} \]

Substituting (1) and (2) into $\E(s^2_Y)$, we obtain \[ \begin{align*} \E(s^2_Y)=\frac{1}{n-1}\left(n(\sigma^2_Y+\mu^2_Y)-n(\sigma^2_Y/n+\mu^2_Y)\right)=\sigma^2_Y, \end{align*} \] which shows that $s^2_Y$ is an unbiased estimator of $\sigma^2_Y$.

To show that $s^2_Y\xrightarrow{p}\sigma^2_Y$, we first consider the following expression: \[ \begin{align*} \frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2=\frac{1}{n}\sum_{i=1}^nY^2_i-\bar{Y}^2. \end{align*} \]

By the law of large numbers, $\frac{1}{n}\sum_{i=1}^nY^2_i\xrightarrow{p}\E(Y^2_i)$ because $\{Y^2_i\}$ are i.i.d. and $\E(Y^4_i)<\infty$. Also note that $\bar{Y}^2\xrightarrow{p}\mu^2_Y$. Thus, \[ \begin{align*} \frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2=\frac{1}{n}\sum_{i=1}^nY^2_i-\bar{Y}^2\xrightarrow{p}(\sigma^2_Y+\mu^2_Y)-\mu^2_Y=\sigma^2_Y. \end{align*} \]

Finally, $s^2_Y=\left(\frac{n}{n-1}\right)\left(\frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2\right)\xrightarrow{p}\sigma^2_Y$ follows because $\frac{n}{n-1}\to1$.

These results suggest that we can estimate $\var(\bar{Y})=\sigma^2_Y/n$ by $\widehat{\var}(\bar{Y})=s^2_Y/n$.

Key Concept 10.2: The Standard Error of $\bar{Y}$

The standard error of $\bar{Y}$ is an estimator of the standard deviation of $\bar{Y}$. The standard error of $\bar{Y}$ is denoted by $\SE(\bar{Y})$ and is given by \[ \SE(\bar{Y})=\hat{\sigma}_{\bar{Y}}=s_Y/n. \]

Example 10.4 For illustrating $\E(s^2_Y) = \sigma^2_Y$ and $s^2_Y \xrightarrow{p} \sigma^2_Y$, we assume that $Y_1, Y_2, \dots, Y_n$ are i.i.d. random variables from the $\chi^2_4$ distribution. Recall that if $Y \sim \chi^2_4$, then $\sigma^2_Y = 8$. In the following simulation exercise, we compute the sample variance $1000$ times for different sample sizes, with $n \in \{30, 100, 200, 500\}$. We then generate histogram plots of the sample variances. The simulation results are shown in Figure 10.3. The figure indicates that, as the sample size increases, the mean of the sample variances gets closer to the true value $8$. Moreover, the sampling distribution becomes more tightly concentrated around the mean.

# The sampling distribution of the sample variance
# Set parameters
reps = 1000 # number of repetitions
sample_sizes = [30, 100, 200, 500]
m = 4 # degrees of freedom
# Set seed for reproducibility
np.random.seed(45)
# Create a 2x2 subplot array
fig, axs = plt.subplots(2, 2)
# Flatten the array of axes for easy iteration
axs = axs.flatten()
# Outer loop (loop over the sample sizes)
for i, n in enumerate(sample_sizes):
    sample_variance = np.zeros(reps) # Initialize the vector of sample variance
    # Inner loop over repetitions
    for j in range(reps):
        x = stats.chi2.rvs(df=m, size=n)
        sample_variance[j] = np.var(x,ddof=1) # compute variance

    # Plot histogram
    ax = axs[i]
    v_mean = np.mean(sample_variance)
    ax.hist(sample_variance, bins=30, color='steelblue', edgecolor='black')
    ax.axvline(x=v_mean, color='red', linestyle='--', linewidth=1.5, 
    label=f'Mean = {v_mean:.2f}')  # Solid vertical line at mean
    ax.set_xlim(0, 18)
    ax.set_xlabel(f'n = {n}')
    ax.legend(frameon=False)
# Adjust layout
plt.tight_layout()
# Show the plot
plt.show()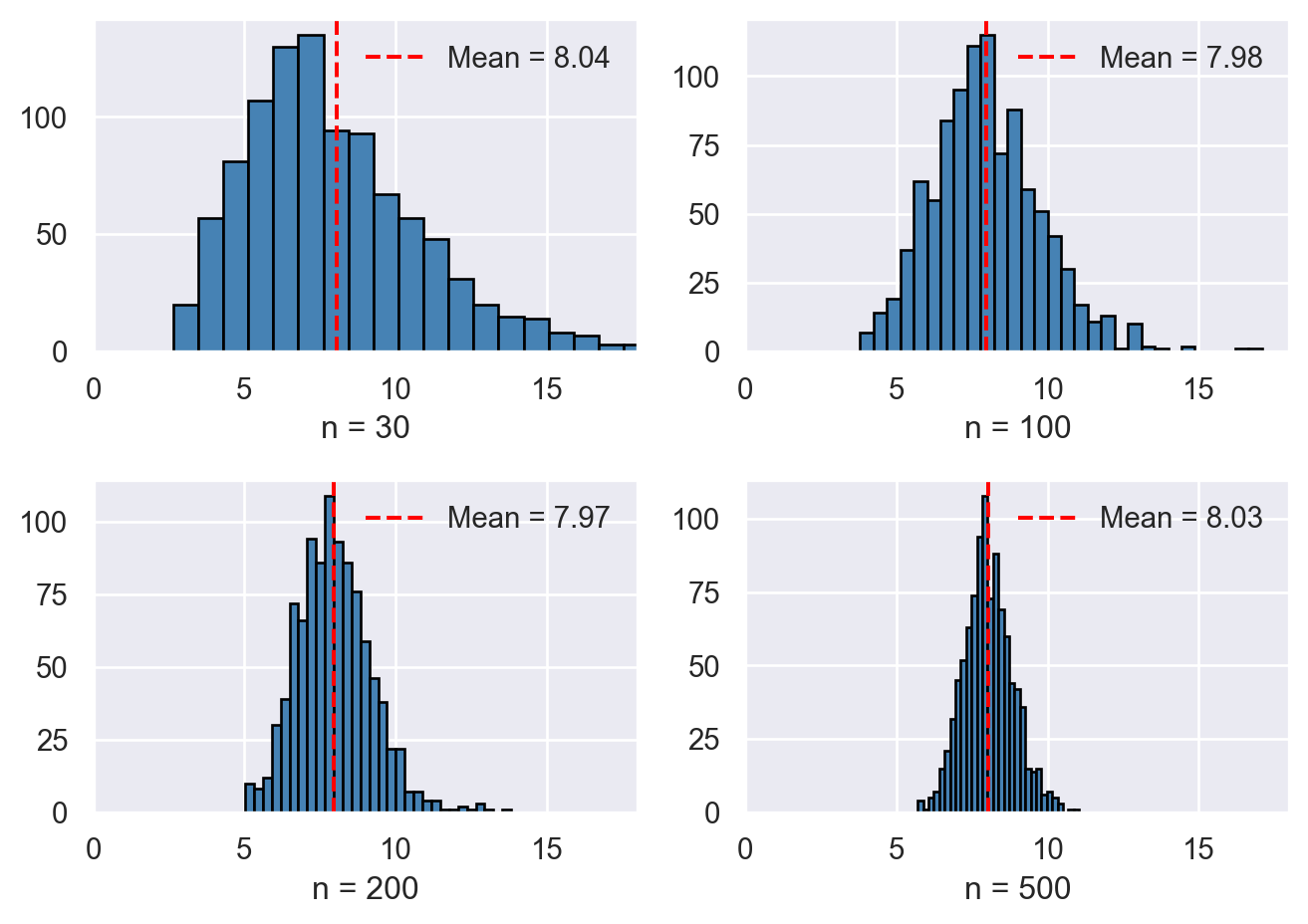

Figure 10.3: The sampling distribution of the sample variance

10.4 Hypothesis tests concerning the population mean

A hypothesis is a claim about some characteristic of a random variable, such as its mean, variance, and some other parameters. We refer to the hypothesis being tested as the null hypothesis, denoted by $H_0$. The scenario in which the null hypothesis does not hold is described by the alternative hypothesis, denoted by $H_1$.

Example 10.5 Let $Y$ denote the hourly earnings of recent college graduates. If we conjecture that, on average, college graduates earn $20 per hour, this translates to $H_0: \mu_Y = 20$. Against this null hypothesis, we can formulate the following alternative hypotheses:

Two-sided alternative hypothesis: $H_1: \mu_Y \ne 20$.
One-sided alternative hypothesis: $H_1: \mu_Y > 20$ or $H_1: \mu_Y < 20$.

The null value (or the hypothesized value) is the specified value of the population parameter under the null hypothesis $H_0$. In this example, the null value is $20.

In hypothesis testing, we use sample data to test the null hypothesis $H_0$ against the alternative hypothesis $H_1$. The goal is to determine whether there is sufficient evidence in the sample to reject the null hypothesis in favor of the alternative. The testing process involves the following steps:

State the null $H_0$ and the alternative $H_1$,
Choose a significance level for the test,
Calculate a test statistics to test $H_0$,
Decide whether to reject $H_0$ or not.

In this process, we can commit two types of errors: Type-I error and Type-II error. We commit Type-I error if we reject the true $H_0$, and Type-II error if we fail to reject the false $H_0$. Since we cannot simultaneously minimize the likelihood of both errors, we choose a significance level, denoted by $\alpha$, for committing the Type-I error, and then work to minimize the likelihood of committing the Type-II error. You can think of the significance level of the test as your tolerance for rejecting a true null hypothesis $H_0$. The conventional significance levels are $1\%$, $5\%$, and $10\%$. For example, if we use $\alpha = 0.05$, then we accept the possibility of rejecting a true null hypothesis $5$ times out of $100$ resamples.

We consider the following $t$ statistic as our test statistic: \[ \begin{align} t &= \frac{\bar{Y} - \mu_Y}{s_{\bar{Y}}}, \end{align} \tag{10.1}\]

where $s_{\bar{Y}} = \sqrt{s_Y^2/n}= s_Y/\sqrt{n}$ is the standard error of $\bar{Y}$. By the CLT introduced in Chapter 9, under $H_0$, the sampling distribution of $t$ statistic can be approximated by the standard normal distribution when $n$ is large, i.e., \[ \begin{align} t &= \frac{\bar{Y} - \mu_Y}{s_{\bar{Y}}}\xrightarrow{d} N(0,1). \end{align} \tag{10.2}\]

We then can use the significance level, the alternative hypothesis, and the distribution of the test statistic to determine the rejection regions.

For $H_1:\mu_Y>20$, the rejection region is $\{t>z_{\alpha}\}$, where $z_{\alpha}$ is the critical value of the standard normal distribution at the significance level $\alpha$.
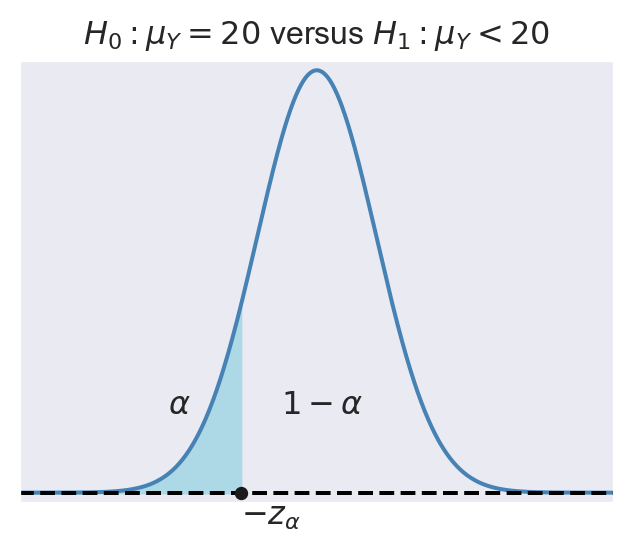
For $H_1:\mu_Y<20$, the rejection region is $\{t<-z_{\alpha}\}$, where $-z_{\alpha}$ is the critical value of the standard normal distribution at the significance level $\alpha$.
For $H_1:\mu_Y\ne20$, the rejection region is $\{|t|>z_{\alpha/2}\}$, where $z_{\alpha/2}$ is the critical value of the standard normal distribution at the significance level $\alpha/2$.

In Figure 10.4, we show the rejection regions according to the type of $H_1$. In the figure, the critical values are $z_{\alpha}$, $-z_{\alpha}$, $-z_{\alpha/2}$, and $z_{\alpha/2}$. The critical value, which is the threshold that separates the rejection region from the non-rejection region, depends on the significance level $\alpha$ and the alternative hypothesis $H_1$:

In the case of $H_1:\mu_Y>20$, the critical value $z_{\alpha}$ is the $1-\alpha$ quantile of the sampling distribution of the test statistic.
In the case of $H_1:\mu_Y<20$, the critical value $-z_{\alpha}$ is the $\alpha$ quantile of the sampling distribution of the test statistic.
If we consider the two-sided alternative hypothesis $H_1:\mu_Y\ne20$, then the critical values are $-z_{\alpha/2}$ and $z_{\alpha/2}$, which are the $\alpha/2$ and $1-\alpha/2$ quantiles of the sampling distribution of the test statistic, respectively.

If the realized value of $t$ is in the rejection region, we reject the null hypothesis $H_0$; otherwise, we fail to reject $H_0$. Intuitively, if the realized value of $t$ is in the rejection region, it means that the sample mean $\bar{Y}$ is far away from the null value $\mu_Y=20$, which suggests that the null hypothesis $H_0$ can not be true.

# Rejection Regions
alpha = 0.05  # Significance level
x = np.linspace(-5, 5, 1000) # Define the x range for plotting

# Upper-tailed rejection region
fig, axs = plt.subplots(figsize=(4, 3))
pdf = stats.norm.pdf(x)
axs.plot(x, pdf, color='steelblue', linestyle='-', lw=1.5)
axs.axhline(0, color='black', linestyle='--')
x_fill = np.linspace(stats.norm.ppf(0.90), 5, 1000)
pdf_fill = stats.norm.pdf(x_fill)
axs.fill_between(x_fill, 0, pdf_fill, color='lightblue')
axs.plot(stats.norm.ppf(0.90), 0, 'ko', markersize=4)
axs.text(-0.6, 0.075, r'$1-\alpha$')
axs.text(2, 0.075, r'$\alpha$')
axs.text(stats.norm.ppf(0.90), -0.03, r'$z_\alpha$')
axs.set_xlim(-5, 5)
axs.set_ylim(-0.01, max(pdf) + 0.01)
axs.xaxis.set_ticks([])  # Remove x-axis numbers
axs.yaxis.set_ticks([]) # Remove y-axis numbers
axs.set_title(r'$H_0:\mu_Y=20$ versus $H_1:\mu_Y>20$')

# Lower-tailed rejection region
fig, axs = plt.subplots(figsize=(4, 3))
axs.plot(x, pdf, color='steelblue', linestyle='-', lw=1.5)
axs.axhline(0, color='black', linestyle='--')
x_fill = np.linspace(-5, stats.norm.ppf(0.10), 1000)
pdf_fill = stats.norm.pdf(x_fill)
axs.fill_between(x_fill, 0, pdf_fill, color='lightblue')
axs.plot(stats.norm.ppf(0.10), 0, 'ko', markersize=4)
axs.text(-0.6, 0.075, r'$1-\alpha$')
axs.text(-2.5, 0.075, r'$\alpha$')
axs.text(-stats.norm.ppf(0.90), -0.03, r'$-z_\alpha$')
axs.set_xlim(-5, 5)
axs.set_ylim(-0.01, max(pdf) + 0.01)
axs.xaxis.set_ticks([])  # Remove x-axis numbers
axs.yaxis.set_ticks([])  # Remove y-axis numbers
axs.set_title(r'$H_0:\mu_Y=20$ versus $H_1:\mu_Y<20$')

# Two-tailed rejection regions
fig, axs = plt.subplots(figsize=(4, 3))
axs.plot(x, pdf, color='steelblue', linestyle='-', lw=1.5)
axs.axhline(0, color='black', linestyle='--')
# Left rejection region
x_fill = np.linspace(-5, stats.norm.ppf(0.05), 1000)
pdf_fill = stats.norm.pdf(x_fill)
axs.fill_between(x_fill, 0, pdf_fill, color='lightblue')
# Right rejection region
x_fill = np.linspace(stats.norm.ppf(0.95), 5, 1000)
pdf_fill = stats.norm.pdf(x_fill)
axs.fill_between(x_fill, 0, pdf_fill, color='lightblue')
axs.plot(stats.norm.ppf(0.05), 0, 'ko', markersize=4)
axs.plot(stats.norm.ppf(0.95), 0, 'ko', markersize=4)
axs.text(-0.6, 0.075, r'$1-\alpha$')
axs.text(-3, 0.07, r'$\alpha/2$')
axs.text(2.5, 0.07, r'$\alpha/2$')
axs.text(stats.norm.ppf(0.95), -0.03, r'$z_{\alpha/2}$')
axs.text(-stats.norm.ppf(0.95), -0.03, r'$-z_{\alpha/2}$')
axs.set_xlim(-5, 5)
axs.set_ylim(-0.01, max(pdf) + 0.01)
axs.xaxis.set_ticks([])  # Remove x-axis numbers
axs.yaxis.set_ticks([])  # Remove y-axis numbers
axs.set_title(r'$H_0:\mu_Y=20$ versus $H_1:\mu_Y\ne20$')

plt.tight_layout()
plt.show()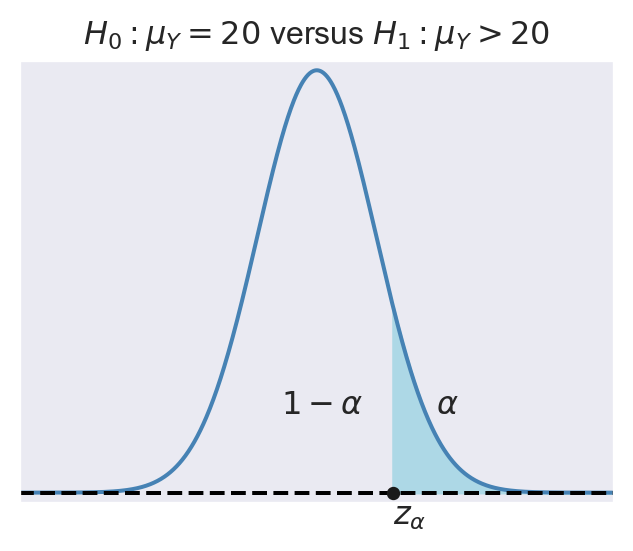

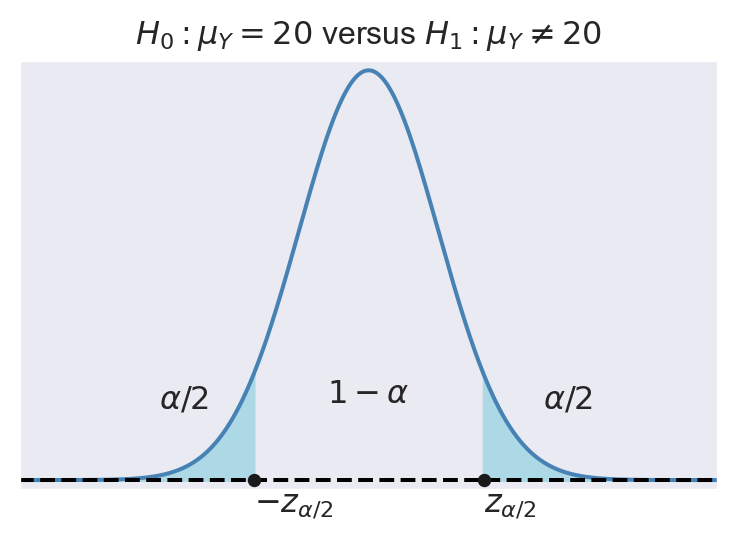
Example 10.6 Assume that $\alpha = 5%$ and the alternative hypothesis is specified as $H_1: \mu_Y \neq 20$. Then, the critical value on the left tail is the $2.5$th percentile of $N(0,1)$, which is $-z_{\alpha/2} = -1.96$, and the critical value on the right tail is the $97.5$th percentile of $N(0,1)$, which is $z_{\alpha/2} = 1.96$. Using Python, we can compute the critical values as follows:

left_critical = stats.norm.ppf(0.025,loc=0,scale=1)
right_critical = stats.norm.ppf(0.975,loc=0,scale=1)
print("Left critical value:", np.round(left_critical,2))
print("Right critical value:", np.round(right_critical,2))

Left critical value: -1.96
Right critical value: 1.96

If we obtain $t=\frac{\bar{Y} - 20}{s_{\bar{Y}}}=2$, then we will reject $H_0$ because the test statistic value is in the rejection region, i.e., $2>z_{\alpha/2}=1.96$.

Instead of using the critical values and the rejection regions to test $H_0$, we can also use the $p$-value.

Definition 10.4 (The $p$-value) The $p$-value is the probability of obtaining a test statistic value that is more extreme than the actual one when the null is correct.

Let $t_{\text{calc}}$ be the value of the test statistic obtained from Equation 10.1. Then, the $p$-value is defined by \[ \begin{align*} \text{$p$-value}= \begin{cases} P_{H_0}\left(t > |t_{\text{calc}}|\right), \quad&\text{for }H_1:\mu_Y>20,\\ P_{H_0}\left(t <-|t_{\text{calc}}|\right), \quad&\text{for }H_1:\mu_Y<20,\\ P_{H_0}\left(|t| > |t_{\text{calc}}|\right), \quad&\text{for }H_1:\mu_Y\ne20, \end{cases} \end{align*} \] where $P_{H_0}$ means the probability is calculated from the distribution of the test statistic under the null hypothesis. Since the asymptotic distribution of $t$ statistic is $N(0,1)$ as shown in Equation 10.2, we have \[ \begin{align*} \text{$p$-value}= \begin{cases} P_{H_0}\left(t > |t_{\text{calc}}|\right)=1-\Phi(|t_{\text{calc}}|), \quad&\text{for }H_1:\mu_Y>20,\\ P_{H_0}\left(t <-|t_{\text{calc}}|\right)=\Phi(-|t_{\text{calc}}|), \quad&\text{for }H_1:\mu_Y<20,\\ P_{H_0}\left(|t| > |t_{\text{calc}}|\right)=2\times\Phi(-|t_{\text{calc}}|), \quad&\text{for }H_1:\mu_Y\ne20. \end{cases} \end{align*} \]

We reject the null hypothesis $H_0$ at the significance level $\alpha$ if the $p$-value is less than $\alpha$. In other words, we reject $H_0$ if the probability of obtaining a test statistic value that is more extreme than the actual one is small enough, which suggests the realized is already in the rejection region.

Example 10.7 Assume that $\alpha=5\%$ and $H_1:\mu_Y\ne20$. Suppose we obtained $t=\frac{\bar{Y} - 20}{s_{\bar{Y}}}=2$. Then, \[ \begin{align*} \text{$p$-value}=P_{H_0}\left(|t| > 2\right)=P_{H_0}\left(t > 2\right)+P_{H_0}\left(t <- 2\right)=2\times\Phi(-2). \end{align*} \] We can compute the $p$-value using Python as follows:

p_value = 2*stats.norm.cdf(-2,loc=0,scale=1)
print("p-value:", np.round(p_value,4) )

p-value: 0.0455

Since $p-$value $=0.045<\alpha=0.05$, we reject $H_0$ at the $5\%$ significance level.

Note that we determine the critical values and $p$-values by assuming that the distribution result in Equation 10.2 holds, which requires a large sample size. That is, the standard normal distribution may not provide a good approximation to the sampling distribution of the t-statistic when the sample size is small. If we assume that $Y_1,\dots,Y_n$ are i.i.d. random variables from $N(\mu_Y,\sigma^2_Y)$, then it can be shown that

\[ \begin{align} t &= \frac{\bar{Y} - \mu_Y}{s_{\bar{Y}}}\sim t_{n-1}, \end{align} \tag{10.3}\]

where $t_{n-1}$ is the Student t distribution with $n-1$ degrees of freedom. The distribution result in Equation 10.3 is exact in the sense that it holds regardless of the sample size.

Recall that when $n > 30$, the $t$-distribution and $N(0,1)$ are very close (as $n$ grows large, the $t_{n-1}$ distribution converges to $N(0,1)$). Thus, as long as the sample size is larger than $30$, we can rely on the standard normal distribution for the critical values and p-values. Therefore, Stock and Watson (2020) conclude that “inferences-hypothesis tests and confidence intervals-about the mean of a distribution should be based on the large-sample normal approximation.”

Key Concept 10.3: Testing $H_0:\mu_Y=\mu_0$ versus $H_1:\mu_Y\ne\mu_0$

Compute the standard error of $\bar{Y}$, $\SE(\bar{Y})=\hat{\sigma}_{\bar{Y}}=s^2_Y/n$.
Compute the t-statistic given in Equation 10.1 under $H_0$. Reject $H_0$ at the $5\%$ significance level if $|t|>1.96$.
Compute $p$-value from $2\times\Phi(-|t_{\text{calc}}|)$, where $t_{\text{calc}}$ is the actual test statistic computed in the second step. Reject $H_0$ at the $5\%$ significance level if the p-value is less than $0.05$.

10.5 Confidence intervals for the population mean

We want to construct an interval for the population mean $\mu_Y$ such that the true value of $\mu_Y$ is contained in the interval with a pre-specified probability.

Definition 10.5 (Confidence interval) Let $\alpha$ be the significance level. Then, a $100(1-\alpha)\%$ confidence interval for the population mean $\mu_Y$ is an interval that contains $\mu_Y$ with probability $1-\alpha$.

Let $\alpha=0.05$. Then, one way to construct the $95\%$ two-sided confidence interval for $\mu_Y$ is to collect all values $\mu_{Y,0}$ that cannot be rejected by the $t$ statistic for testing $H_0:\mu_Y=\mu_{Y,0}$ versus $H_1:\mu_Y\ne\mu_{Y,0}$ at the $5\%$ significance level. In other words, we collect all values $\mu_{Y,0}$ for which the test statistic $t$ in Equation 10.1 is not in the rejection region, i.e., $|t|\le 1.96$. This construction implies that the 95% two-sided confidence interval for $\mu_Y$ corresponds to the set of values satisfying \[ \begin{align*} P\left(\left\{\mu_Y: \left|\frac{\bar{Y} - \mu_Y}{s_Y/\sqrt{n}}\right| \le 1.96\right\}\right) = 0.95. \end{align*} \]

We can express the set $\left\{\mu_Y: \left|\frac{\bar{Y} - \mu_Y}{s_Y/\sqrt{n}}\right| \le 1.96\right\}$ as follows: \[ \begin{align*} \left\{\mu_Y:\left|\frac{\bar{Y} - \mu_Y}{s_Y/\sqrt{n}}\right|\le 1.96\right\}&=\left\{\mu_Y:-1.96\le \frac{\bar{Y}-\mu_Y}{s_Y/\sqrt{n}}\le 1.96\right\}\\ &=\left\{\mu_Y:-\bar{Y} - 1.96\times s_Y/\sqrt{n}\le -\mu_Y \le -\bar{Y} + 1.96\times s_Y/\sqrt{n}\right\}\\ &=\left\{\mu_Y: \bar{Y} - 1.96\times s_Y/\sqrt{n} \le \mu_Y \le \bar{Y} + 1.96\times s_Y/\sqrt{n}\right\}\\ &=\left\{\mu_Y: \bar{Y} \pm 1.96 \times \text{SE}(\bar{Y})\right\}. \end{align*} \]

Thus, the lower bound of the confidence interval is $\bar{Y} - 1.96 \times \text{SE}(\bar{Y})$ and the upper bound is $\bar{Y} + 1.96 \times \text{SE}(\bar{Y})$, where $\text{SE}(\bar{Y})=s_Y/\sqrt{n}$ is the standard error of $\bar{Y}$. If we choose another pre-specified probability, say $90\%$ or $99\%$, then we only need to change the critical value in the formula, i.e., \[ \begin{align*} &\{\mu_Y: \bar{Y} \pm 1.64 \times \text{SE}(\bar{Y})\}\quad\text{or}\quad \{\mu_Y: \bar{Y} \pm 2.58 \times \text{SE}(\bar{Y})\}. \end{align*} \]

The confidence interval can be used to test the null hypothesis $H_0:\mu_Y = \mu_0$ against the alternative hypothesis $H_1:\mu_Y \ne \mu_0$. Based on the 95% confidence interval, we reject the null hypothesis at the $5\%$ significance level if the hypothesized value $\mu_0$ is not contained within the interval; otherwise, we fail to reject the null hypothesis.

Note that we construct the the $95\%$ confidence interval $\{\mu_Y: \bar{Y} \pm 1.96 \times \text{SE}(\bar{Y})\}$ by using the critical values from the standard normal distribution. That is, our confidence interval is based on the central limit theorem result in Equation 10.2, which requires a large sample size. In the following simulation exercise, we compute nsim=5000 confidence intervals for different sample sizes and then determine the percentage of intervals that includes $\mu_Y$. As the sample size increases, we expect this percentage to approach $95\%$.

def confidence_int(rvgen, n, nsim=5000, alpha=0.05, mu=None, seed=None, **kwargs):
    """
    Inputs:
    - rvgen: Random variable generator, e.g., np.random.normal
    - n: Sample size, possibly a list
    - nsim: Number of iterations, default 5000
    - alpha: Significance level, default 0.05 (95% confidence level)
    - mu: Population mean
    - seed: Seed for random number generator for reproducibility
    - kwargs: Additional arguments to be passed to rvgen
    """
    # Set the random seed for reproducibility
    if seed is not None:
        np.random.seed(seed)
    
    # Verify arguments
    if rvgen is None or not callable(rvgen) or n is None or mu is None:
        raise ValueError("Invalid input arguments")

    # Setup output array
    results = np.zeros(len(n))

    # Loop through different sample sizes
    for i in range(len(n)):
        CP = np.zeros(nsim)

        # Simulation loop
        for j in range(nsim):
            # Generate random sample
            x = rvgen(size=n[i], **kwargs)
            
            # Calculate the confidence interval
            xbar = np.mean(x)
            s = np.std(x, ddof=1)  # Sample standard deviation
            lower = xbar - 1.96 * (s / np.sqrt(n[i]))
            upper = xbar + 1.96 * (s / np.sqrt(n[i]))
            CP[j] = 1 if (lower < mu < upper) else 0

        results[i] = np.mean(CP)

    return results

We assume that the random samples $Y_1, \dots, Y_n$ are generated from three different distributions: (i) $N(0,1)$, (ii) $\chi^2_3$, and (iii) the uniform distribution over the interval $(0,1)$. The simulation results are given in Table 10.1. The results indicate that the percentages get closer to $95\%$ as the sample size increases from $n =30$ to $n=500$.

# Population distribution: standard normal distribution
p1 = confidence_int(np.random.normal, n=[30, 100, 500], mu=0, loc=0, scale=1, seed=42)

# Population distribution: chi-squared distribution
p2 = confidence_int(np.random.chisquare, n=[30, 100, 500], mu=3, df=3, seed=42)

# Population distribution: uniform distribution
p3 = confidence_int(np.random.uniform, n=[30, 100, 500], mu=0.5, low=0, high=1, seed=42)

# Simulation results for the confidence intervals
df = pd.DataFrame([p1, p2, p3])
df.index = ["Normal", "Chi-squared", "Uniform"]
df.columns = ["n=30", "n=100", "n=500"]
df

Table 10.1: Simulation Results

	n=30	n=100	n=500
Normal	0.9326	0.9454	0.9538
Chi-squared	0.9300	0.9390	0.9474
Uniform	0.9368	0.9436	0.9514

Key Concept 10.4: Confidence Intervals for $\mu_Y$

The $95\%$ two-sided confidence interval for $\mu_Y$ is an interval that includes $\mu_Y$ in $95\%$ of all possible random samples. When the sample size is large, we have:

$90\%$ two-sided confidence interval for $\mu_Y$: $\{\mu_Y: \bar{Y} \pm 1.64 \times \text{SE}(\bar{Y})\}$.
$95\%$ two-sided confidence interval for $\mu_Y$: $\{\mu_Y: \bar{Y} \pm 1.96 \times \text{SE}(\bar{Y})\}$.
$99\%$ two-sided confidence interval for $\mu_Y$: $\{\mu_Y: \bar{Y} \pm 2.58\times \text{SE}(\bar{Y})\}$.

10.6 Comparing means from different populations

Let $\mu_w$ be the mean hourly earnings in the population of women recently graduated from college and $\mu_m$ be the mean hourly earnings in the population of men recently graduated from college. We want to formulate hypotheses for the difference between the mean earnings of female and male college graduates. The null hypothesis and the two-sided alternative hypothesis are \[ \begin{align*} H_0: \mu_m - \mu_w = d_0 \quad \text{vs.}\quad H_1: \mu_m - \mu_w \ne d_0, \end{align*} \] where $d_0$ is the hypothesized known value.

Let $\bar{Y}_m$ be the sample average annual earnings for men and $\bar{Y}_w$ be the sample average annual earnings for women. Then, an estimator of $\mu_m - \mu_w$ is $\bar{Y}_m - \bar{Y}_w$. Due to simple random sampling, we can invoke the central limit theorem to claim that $\bar{Y}_m \sim N(\mu_m,\,\frac{\sigma^2_m}{n_m})$ and $\bar{Y}_w \sim N(\mu_w,\,\frac{\sigma^2_w}{n_w})$, where $\sigma^2_m$ and $\sigma^2_w$ are population variances of earnings, and $n_m$ and $n_w$ are sample sizes for men and women, respectively. Since a weighted average of two normal random variables is itself normally distributed, we have \[ \begin{align*} (\bar{Y}_m - \bar{Y}_w)\sim N\left(\mu_m - \mu_w,\, \frac{\sigma^2_m}{n_m} + \frac{\sigma^2_w}{n_w}\right). \end{align*} \] Analogous to the test statistic in Equation 10.1, the t-statistic is \[ \begin{align*} t &= \frac{(\bar{Y}_m - \bar{Y}_w) - d_0}{\sqrt{\frac{s_{Y_m}^2}{n_m} + \frac{s_{Y_w}^2}{n_w}}}, \end{align*} \] where $s^2_{Y_m}$ and $s^2_{Y_w}$ are sample variances for men and women, respectively. If both $n_m$ and $n_w$ are large, then this t-statistic has a standard normal distribution under the null hypothesis: \[ \begin{align*} t &= \frac{(\bar{Y}_m - \bar{Y}_w) - d_0}{\sqrt{\frac{s_{Y_m}^2}{n_m} + \frac{s_{Y_w}^2}{n_w}}}\sim N(0,1). \end{align*} \]

These result suggests that we can follow the same steps given in Key Concept 10.3 to test the null hypothesis.

Finally, the $95\%$ confidence interval for $\mu_m - \mu_w$ is \[ \begin{align*} &\{(\mu_m - \mu_w): (\bar{Y}_m - \bar{Y}_w) \pm 1.96 \times \SE(\bar{Y}_m - \bar{Y}_w)\}, \end{align*} \] where $\SE(\bar{Y}_m - \bar{Y}_w)=\sqrt{\frac{s_{Y_m}^2}{n_m} + \frac{s_{Y_w}^2}{n_w}}$ is the standard error of $(\bar{Y}_m - \bar{Y}_w)$.

For illustration, we use a dataset on the hourly earnings of college-educated, full-time workers aged 25–34 in the United States for the years 1996 and 2015. The CPS96_15.xlsx file contains the data on the following variables:

female: 1 if female; 0 if male
year: Year of observation (1996 or 2015)
ahe: Average hourly earnings in dollars
bachelor: 1 if worker has a bachelor’s degree; 0 if worker has a high school degree
age: Age

We use the following code chunk to import the data and display the first five rows for college graduates.

# Import the data
cps = pd.read_excel("data/CPS96_15.xlsx")
# Filter the data for college graduates (bachelor's degree holders)
cps = cps[cps.bachelor==1]
# The first five rows of the dataset
cps.head()

	year	ahe	bachelor	female	age
2	1996	9.615385	1	1	27
3	1996	11.217949	1	0	26
4	1996	9.615385	1	1	28
5	1996	14.423077	1	0	32
7	1996	25.000000	1	0	31

In the following code chunk, we compute the average wage gap $\bar{Y}_m - \bar{Y}_w$ and then the $95\%$ two-sided confidence interval $(\bar{Y}_m - \bar{Y}_w) \pm 1.96 \times \SE(\bar{Y}_m - \bar{Y}_w)$ for each year. The results are shown in Table 10.1. The average hourly earnings for male college graduates were $16.5 and $28 in 1996 and 2015, respectively. In comparison, female graduates earned an average of $13.9 in 1996 and $23 in 2015. Therefore, the average earnings gap was $2.05 in 1996 and widened to $4.19 in 2015. The estimated confidence intervals for the average earnings gaps are (2.05, 3.085) and (4.192, 5.841) in 1996 and 2015, respectively.

# Group data by gender and year and compute mean, standard deviation, and number of observations for each group
avgs = cps.groupby(['female', 'year']).agg(
    Y_bar=('ahe', 'mean'),
    s=('ahe', 'std'),
    n=('ahe', 'size')
).reset_index()

# Split the dataset by gender
male = avgs[avgs['female'] == 0]
female = avgs[avgs['female'] == 1]

# Rename columns of both splits
male.columns = ['Sex', 'Year', 'Y_bar_m', 's_m', 'n_m']
female.columns = ['Sex', 'Year', 'Y_bar_f', 's_f', 'n_f']

# Merge the male and female data on 'Year'
merged = pd.merge(male, female, on='Year')

# Estimate gender gaps
gap = merged['Y_bar_m'] - merged['Y_bar_f']

# Compute standard errors for the gaps
gap_se = np.sqrt(merged['s_m']**2 / merged['n_m'] + merged['s_f']**2 / merged['n_f'])

# Compute confidence intervals 
gap_ci_l = gap - 1.96 * gap_se
gap_ci_u = gap + 1.96 * gap_se

# Combine results into a DataFrame
result = pd.DataFrame({
    'Year': merged['Year'],
    'Y_bar_m': merged['Y_bar_m'],
    's_m': merged['s_m'],
    'n_m': merged['n_m'],
    'Y_bar_f': merged['Y_bar_f'],
    's_f': merged['s_f'],
    'n_f': merged['n_f'], 
    'Gap': gap,
    'SE(GAP)': gap_se,
    'CI_Lower': gap_ci_l,
    'CI_Upper': gap_ci_u
})

# Print the results with 3 decimal places
result.round(3)

Table 10.2: The hourly earnings of working college graduates

	Year	Y_bar_m	s_m	n_m	Y_bar_f	s_f	n_f	Gap	SE(GAP)	CI_Lower	CI_Upper
0	1996	16.459	7.575	1387	13.892	5.912	1232	2.567	0.264	2.050	3.085
1	2015	28.055	14.366	1917	23.039	11.218	1816	5.016	0.421	4.192	5.841

10.7 Scatterplots, the sample covariance, and the sample correlation

A scatterplot is a plot of observations on two variables. We use the scatter plot to explore the relationship between two variables. For example, Figure 10.5 displays the scatterplot of the average test scores against the average student-teacher ratios for 420 California school districts. Each point in the figure represents an $(X, Y)$ pair for a school district, where $X$ is the average student-teacher ratio, and $Y$ is the average test score. The scatterplot in Figure 10.5 indicates a negative relationship between the average student-teacher ratio and the average test score. That is, as the student-teacher ratio increases, the average test score tends to decrease.

# The scatterplot of test score and student–teacher ratio
# Import the data
CAschool = pd.read_csv('data/caschool.csv')
# Create a scatterplot
fig, axs = plt.subplots(figsize=(5.5,3.5))
axs.scatter(CAschool.str, CAschool.testscr, color='steelblue', s=15)
axs.set_xlabel("Student–teacher ratio")
axs.set_ylabel("Test score")
plt.show()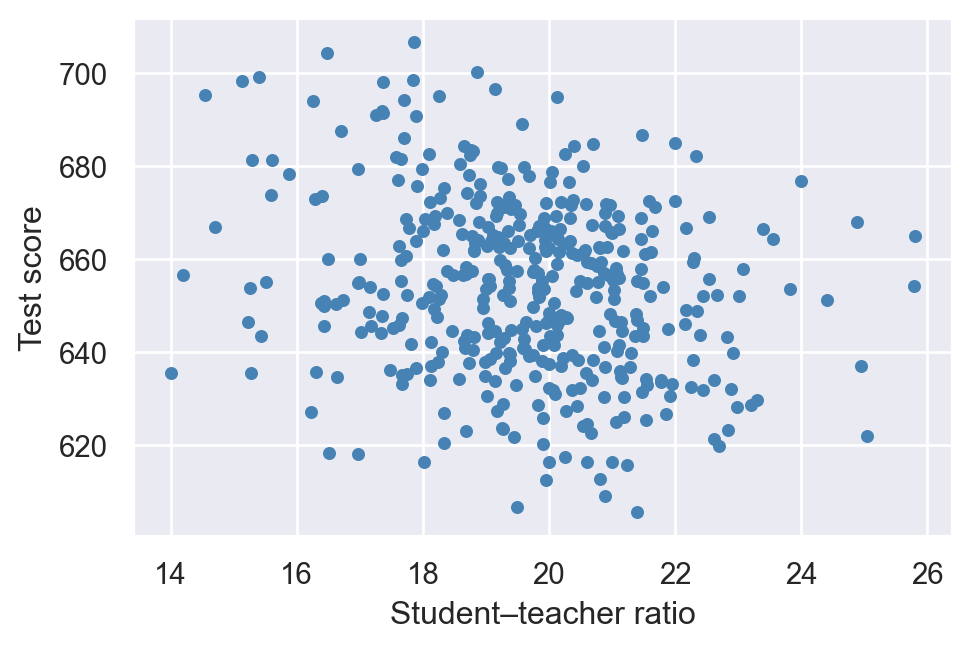

Figure 10.5: The scatterplot of test score and student–teacher ratio

Recall that covariance and correlation are measures linear relationship between two variables $X$ and $Y$. These measures can be estimated by their sample counterparts. Let $(X_i,Y_i)$ for $i=1,2,\dots,n$ be a sample of data on $X$ and $Y$. Then, the sample covariance, denoted by $s_{XY}$, is \[ \begin{align*} s_{XY} &= \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y}). \end{align*} \] The sample correlation coefficient, or sample correlation, denoted by $r_{XY}$, is \[ \begin{align*} r_{XY} &= \frac{s_{XY}}{s_Xs_Y}, \end{align*} \] where $s_X$ and $s_Y$ are the sample standard deviations of $X$ and $Y$, respectively.

Both sample covariance and sample correlation coefficient are consistent estimators, i.e., $s_{XY}\xrightarrow{p}\sigma_{XY}$ and $r_{XY}\xrightarrow{p}\text{corr}(X,Y)$.

The sample correlation coefficient shows the strength of the linear relationship between $X$ and $Y$. As in the case of population correlation coefficient, $r_{XY}$ is unit free and satisfies $|r_{XY}|<1$. In a scatter plot, if points are tightly clustered around a stright line, then we would expect $r_{XY}$ to be around $\pm1$, depending on the slope of the line.

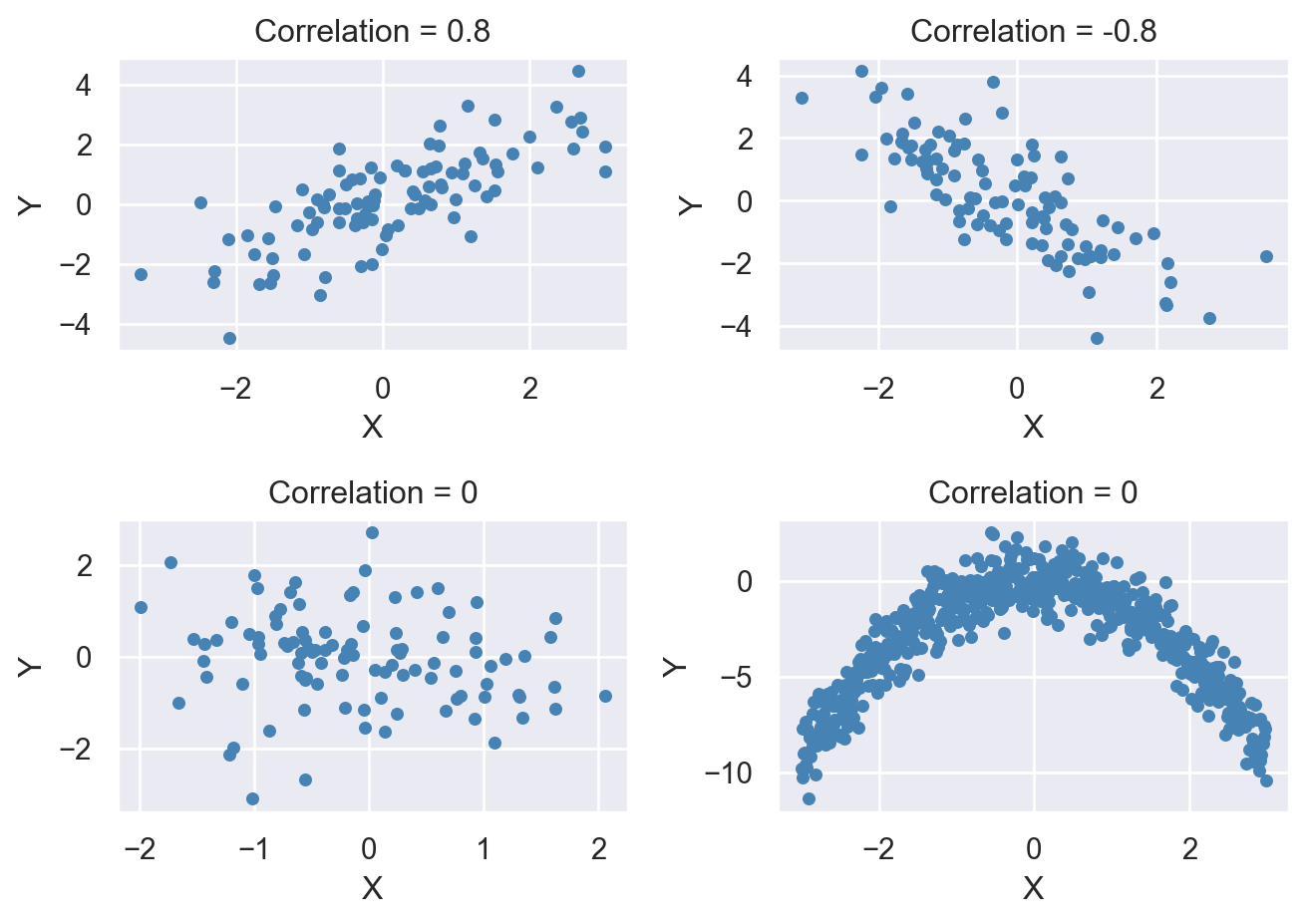
In Figure 10.6, we show four correlation coefficients for four hypothetical data sets. Note that the last plot illustrates a non-linear relationship between $X$ and $Y$, even though the correlation coefficient between $X$ and $Y$ is zero.

# The scatterplots for four hypothetical data sets
# Set random seed
np.random.seed(45)
# Positive correlation: 0.8
mean = [0, 0]
cov_positive = [[2, 2], [2, 3]]
data1 = np.random.multivariate_normal(mean, cov_positive, 100)

# Negative correlation: -0.8
cov_negative = [[2, -2], [-2, 3]]
data2 = np.random.multivariate_normal(mean, cov_negative, 100)

# No correlation
cov_no_corr = [[1, 0], [0, 1]]
data3 = np.random.multivariate_normal(mean, cov_no_corr, 100)

# No correlation (quadratic relationship)
X = np.arange(-3, 3, 0.01)
Y = -X**2 + np.random.normal(size=len(X))
data4 = np.column_stack((X, Y))

# Create a 2x2 grid for plots
fig, axs = plt.subplots(2, 2)

# Plot datasets
axs[0, 0].scatter(data1[:, 0], data1[:, 1], color='steelblue', s=15)
axs[0, 0].set_xlabel('X')
axs[0, 0].set_ylabel('Y')
axs[0, 0].set_title('Correlation = 0.8')

axs[0, 1].scatter(data2[:, 0], data2[:, 1], color='steelblue', s=15)
axs[0, 1].set_xlabel('X')
axs[0, 1].set_ylabel('Y')
axs[0, 1].set_title('Correlation = -0.8')

axs[1, 0].scatter(data3[:, 0], data3[:, 1], color='steelblue', s=15)
axs[1, 0].set_xlabel('X')
axs[1, 0].set_ylabel('Y')
axs[1, 0].set_title('Correlation = 0')

axs[1, 1].scatter(data4[:, 0], data4[:, 1], color='steelblue', s=15)
axs[1, 1].set_xlabel('X')
axs[1, 1].set_ylabel('Y')
axs[1, 1].set_title('Correlation = 0')

plt.tight_layout()
plt.show()

Figure 10.6: The scatterplots for four hypothetical data sets